Floating Point
소수점의 위치가 고정되어 있지 않는 수로 표현하는 컴퓨터 연산. 이진 소수점 왼쪽에 한 자리 숫자만 나오는 형태로 표현한다. 이진수로 나타내면 다음과 같다.
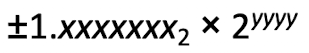
고정 소수점에 비교했을 때 표현할 수 있는 범위가 넓어지지만, 오차가 발생할 수 있다.
IEEE 754 Format

S: Sign bit (0 -> +, 1 -> -)
Normalize significand : 1.0 <= 1 + Fraction <= 2.0
Exponent : actual exponent + Bias (Single-Precision : 127, Double-Precision : 1023)
Denormalized and Special Value
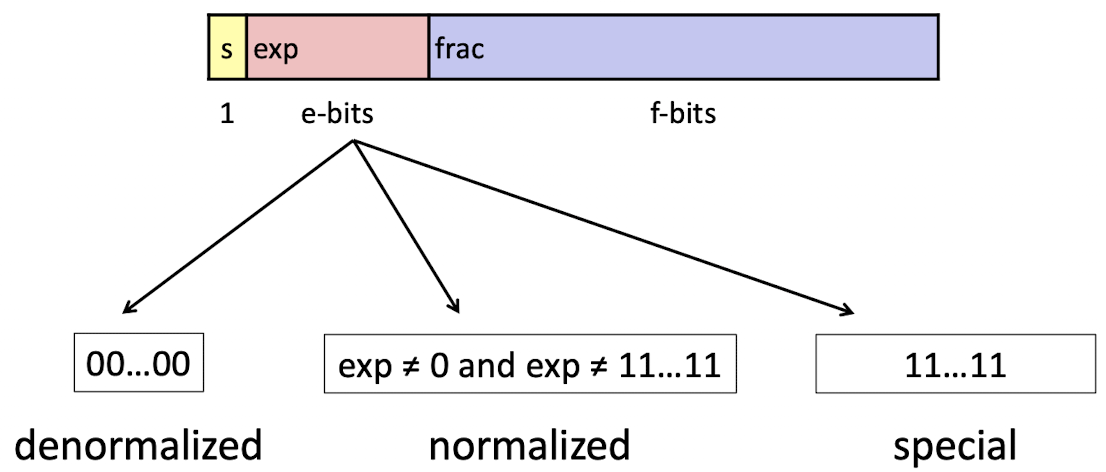
- Exponent 00...00 과 11...11은 각각 0 또는 0에 매우 가까운 수 그리고 무한대 또는 NaN을 표현하기 위해 reserved 되어 있다.
- Denormal Numbers

- Infinities and NaNs

Single-Precision Range

Double-Precision Range

Floating-Point Precision

가수부를 십진수로 표현한 값에 밑이 10인 로그를 취하면 소수점 이하 몇 자리까지 정확하게 표현할 수 있는지 대략 가늠할 수 있다.
23*0.3은 6.9이고, 52*0.3은 15.6이기 때문에 Single Precision인 경우 소수점 이하 대략 6개까지 정확하게 표현 가능 하고, Double Precision인 경우 소수점 이하 대략 15개 까지 정확하게 표현 할 수 있다.
#include <iostream>
#include <iomanip>
#define endl '\n'
using namespace std;
void output()
{
float fnum = 1234567891234567891.0f;
double dnum = 1234567891234567891.0l;
cout << setprecision(18) << fnum << endl;
cout << setprecision(18) << dnum << endl;
}
int main(void)
{
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
output();
return 0;
}
/*
output:
1.23456793955060941e+18
1.23456789123456794e+18
*/Floating-Point Addition

1. 두 피연산자의 지수 같게 맞추기
2. significand끼리 더하기
3. 정규화, 오버플로 및 언더플로 확인
4. 반올림, 필요 시 재정규화
Floating-Point Multiplication

1. 지수끼리 더하기
2. significands끼리 곱하기
3. 정규화, 오버플로 및 언더플로 확인
4. 반올림, 필요 시 재정규화
5. 부호 결정
'Computer Science > Computer Architecture' 카테고리의 다른 글
| [Computer Architecture] Pipelining and Hazards (파이프라이닝과 해저드) (0) | 2024.08.01 |
|---|---|
| [Computer Architecture] CPU Datapath (CPU 데이터패스) (0) | 2024.07.28 |
| [Computer Architecture] Integer Arithmetic (정수 연산) (0) | 2024.07.11 |
| [Computer Architecture] CPU Operation (CPU 작동 원리) (0) | 2024.07.07 |
| [Computer Architecture] Performance (성능) (0) | 2024.07.07 |



